2017计划

Posted on 2017-04-26 Edited on 2019-12-17 In 在人间 Disqus:

锻炼

每天早起
🏃十公里
锻炼上肢力量，引体向上，俯卧撑
健康用眼

Java skill大杂烩

Posted on 2017-04-25 Edited on 2019-12-17 In 我的大学 Disqus:

SKILLS

J2EE

J2EE(Servlet/Concurrence/RMI/JMS/JMX/JDBC…)
Framework(Spring/Struts/Hibernate/Ibatis…)
Weapon(Zookeeper/ActiveMQ/Ant/Maven…)
Server(Nginx/Resin/JBoss/Apache/Jetty…)

《java并发编程的艺术》笔记

Posted on 2017-04-01 Edited on 2019-12-17 In 我的大学 Disqus:

使用并发带来的挑战和解决方案

上下文切换

切换定义：某个线程从上一次（使用CPU时间片）保存状态退出执行到下一次加载执行

影响：切换带来开销

评估：Lmbench3 测量切换时长，vmstat 测量切换次数

解决：无锁并发（如取模分片），CAS算法，避免创建不必要线程，单线程多任务（协程）

实战：减少web容器配置的maxThreads （根据实际情况确定）

死锁

原因：互相等待对方释放锁

场景：异常导致没有到释放环节，或者释放本身异常

解决：避免一个线程同时获取多个锁、占用多个资源，尝试定时锁

硬软件资源限制

示例：带宽、硬盘读写、CPU速度，数据库、socket连接数

问题：并行退化为串行，额外增加了切换开销

解决：集群增加资源，池复用资源，确定并发数时考虑资源限制/瓶颈

* 强烈建议多使用JDK并发包提供的并发容器和工具类 *

底层实现原理

JVM&CPU指令

volatile

如果一个字段被声明成volatile，Java线程内存模型确保所有线程看到这个变量的值是一致的
volotile变量写操作会多一个lock指令：将当前处理器缓存数据写回系统内存，一个处理器的缓存回写到内存会导致其他处理器的缓存无效
处理器使用嗅探技术保证它的内部缓存、系统内存和其他处理器的缓存的数据在总线上保持一致。

使用优化：jdk7引入的LinkedTransferQueue使用追加字节方式，使得队列头尾节点大小刚好符合处理器缓存一个缓存行大小（如64字节），使得头尾节点位于不同缓存行，修改时不互相影响（锁定缓存行），从而加快入队、出队并发速率

synchronized

3种形式

普通同步方法，锁当前实例对象
静态同步方法，锁对应class对象
同步方法块，括号中配置对象

monitorenter指令是在编译后插入到同步代码块的开始位置，而monitorexit是插入到方法结束处和异常处，JVM要保证每个monitorenter必须有对应的monitorexit与之配对。任何对象都有一个monitor与之关联，当一个monitor被持有后，它将处于锁定状态。线程执行到monitorenter指令时，将会尝试获取对象所对应的monitor的所有权，即尝试获得对象的锁

不同锁状态

无锁
偏向锁
- 场景：大部分情况下锁总是被同一线程多次获得
- 解决：对象头MarkWord存储对应锁线程id，以后该线程进入和退出同步块时不需要进行CAS操作来加锁和解锁
- 释放锁：其它线程竞争该锁时才释放，偏向锁释放需要等待全局安全点
轻量级锁
- 使用自旋来竞争
重量级锁

Mac重装系统

Posted on 2016-11-15 Edited on 2019-12-17 In 我的大学 Disqus:

关于备份

可以用外部存储或网络备份，也可以用磁盘工具单独分一个区用来备份

关于重装

关机后，开机时（开机音乐响后）按住command+R，如果不小心看到只有一个带感叹号文件夹在闪，可以开机后按住command+option+P+R,然后再开机按住command+R

开机后可选择进入磁盘工具，格式化原系统分区；然后退出磁盘工具，选择重新安装系统，注意需要有靠谱网络连接（实测不稳定出现2003F等错误后可关机重复操作，直至下载进度条完成）

软件安装与配置

码农必备xcode command tools

可使用xcode-select -p查看是否已安装

也可直接敲gcc命令，mac会聪明的自动弹出安装对话框，选择安装即可

安装后亲切的git等命令就可以用了

软件管理必备brew

使用mac自带“终端”程序，敲入

1	/usr/bin/ruby -e "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/master/install)”

即完成brew安装。

~~使用brew cask可方便的安装一些GUI软件，可考虑加上~~ 新版不需要了

1	brew install caskroom/cask/brew-cask

brew操作过程中可能会遇到github API报错（如果brew源未更改的话）

1	Error: GitHub API Error: API rate limit exceeded for 103.37.140.11.

根据命令行提示去github申请单独token即可

使用国内软件源

cd "$(brew --repo)"
git remote set-url origin https://mirrors.ustc.edu.cn/brew.git
cd "$(brew --repo)/Library/Taps/homebrew/homebrew-core"
git remote set-url origin https://mirrors.ustc.edu.cn/homebrew-core.git
brew update -v

常用软件

#替换终端
brew cask install iterm2
#替换浏览器
brew cask install google-chrome
#开发
brew cask install java
brew install maven
brew install jetty
brew install vim --with-lua --with-override-system-vi
#brew cask install android-studio
brew cask install intellij-idea
brew install wget
#虚拟机，安装Windows用
brew cask install virtualbox virtualbox-extension-pack
brew cask install the-unarchiver
brew cask install mplayerx
#输入法
brew cask install sogouinput
open /usr/local/Caskroom/sogouinput/3.8.0.2054/安装搜狗输入法.app

git库访问权限支持

1
2
3

ssh-keygen -t rsa -b 4096 -C "xxx@gmail.com"
#拷贝公钥
pbcopy < ~/.ssh/id_rsa.pub

goproxy

编译安装比较纠结（“GoProxy 对 golang 周边库做了一些修改”），所以直接下载编译好的包比较方便

简易教程

访问https://github.com/phuslu/goproxy-ci/releases/latest下载最新版，如goproxy_macos_amd64-r1419.tar.bz2，文件托管在amazonaws.com，会有点慢

查看appid可访问https://console.cloud.google.com/home/dashboard

导入代理自动切换规则可以参考https://github.com/gfwlist/gfwlist

mkdir goproxy
cd goproxy
#先下载gae服务器程序，用来上传到gae平台，之前已经部署过的话可以跳过
#上传成功，请不要忘记编辑 gae.user.json 把你的appid填进去
wget https://github.com/phuslu/goproxy-ci/releases/download/r1419/goproxy-gae-r65.zip
unzip goproxy-gae-r65.zip
cd goproxy-r65
python uploader.py
#然后是下载本地客户端，这里下载的是命令行形式的，也可以下载mac app版本
wget https://github.com/phuslu/goproxy-ci/releases/download/r1419/goproxy_macos_amd64-r1419.tar.bz2
tar zxvf goproxy_macos_amd64-r1419.tar.bz2
#编辑完gae.json就可以运行了
vim gae.json
sudo ./goproxy -v=2
#下载SwitchyOmega插件对应的备份配置，然后导入插件
wget https://raw.githubusercontent.com/pengjunlong/goagent/master/local/SwitchyOptions.bak

chrome设置

登录以同步设置、扩展、书签等
SwitchyOmega扩展用来配合科学上网，

配置在线恢复：
http://switchysharp.com/file/SwitchyOptions.bak

配置自动切换：
https://raw.githubusercontent.com/gfwlist/gfwlist/master/gfwlist.txt

dotfile管理

https://github.com/skwp/dotfiles

从github上的介绍，这个“Yet Another Dotfile Repo”包含了vim、zsh相关的很多优秀插件和配置，mac的话还会帮你安装iterm2配色方案，当然有的配置可能不太符合个人原有使用习惯

1	sh -c "`curl -fsSL https://raw.githubusercontent.com/skwp/dotfiles/master/install.sh `"

启用iterm2中的Solarized Colors

Go to Profiles => Colors => Load Presets to pick Solarized Dark.

hexo安装

#安装hexo
brew install node
npm install -g hexo-cli
#下载博客hexo分支
git clone -b hexo --single-branch git@github.com:pengjunlong/pengjunlong.github.io.git hexo
cd hexo/
npm install
#下载主题
git clone https://github.com/iissnan/hexo-theme-next themes/next
git status
git checkout themes/
#运行
hexo s -w

增加了一个hexo-admin插件

Posted on 2016-08-01 Edited on 2019-12-17 In 我的大学 Disqus:

https://hexo.io/plugins/

https://github.com/jaredly/hexo-admin

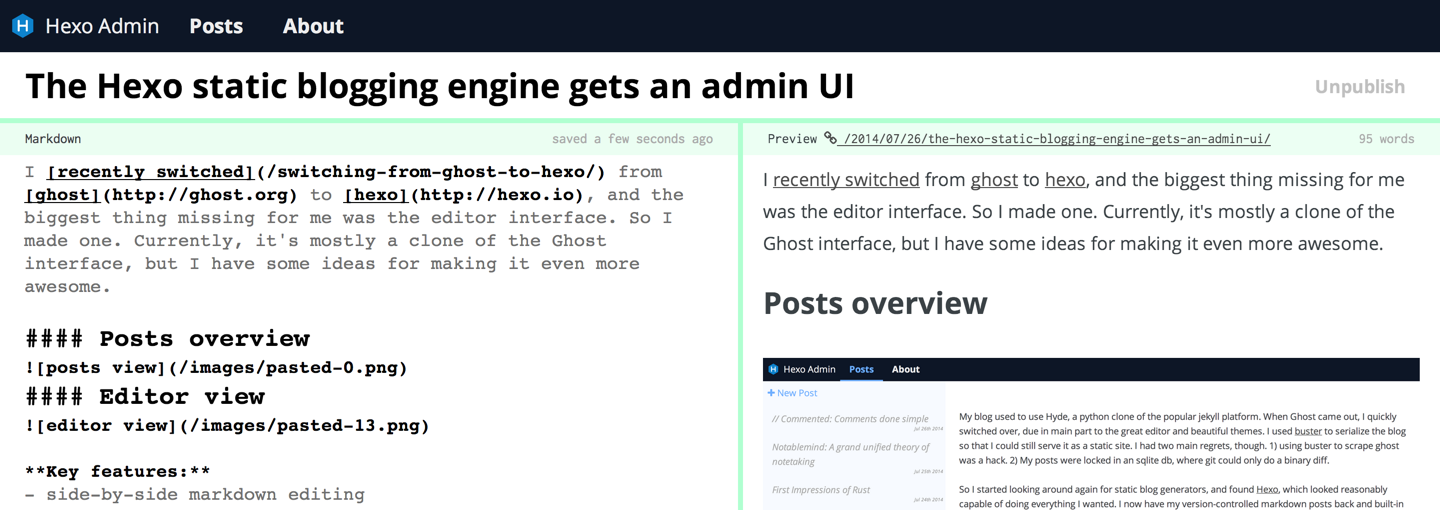
Edit your content in style with this integrating blogging environment.

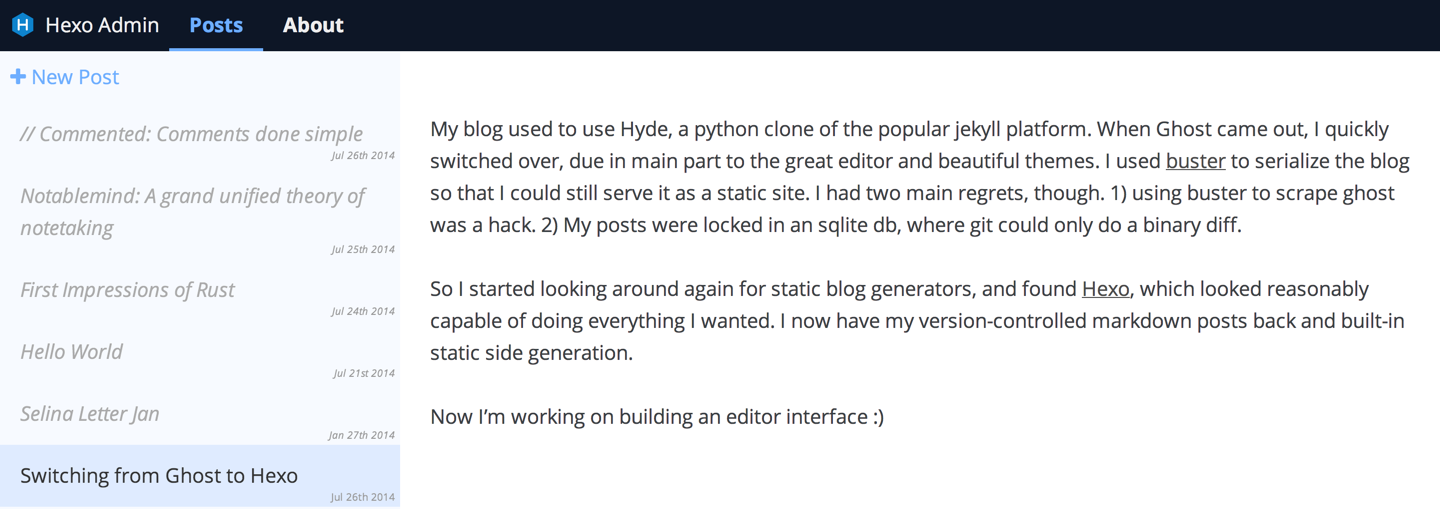
看着效果不错，应该比命令行new直观点

具体添加插件步骤

1
2
3

npm install --save hexo-admin
hexo server -d
open http://localhost:4000/admin/

PHP数组函数性能分析

Posted on 2016-04-27 Edited on 2019-12-17 In 我的大学 Disqus:

List of Big-O for PHP functions

存在所有PHP内置函数的理论（或实际）时间复杂度列表吗？

Since it doesn’t seem like anyone has done this before I thought it’d be good idea to have it for reference somewhere. I’ve gone though and either via benchmark or code-skimming to characterize the array_* functions. I’ve tried to put the more interesting Big-O near the top. This list is not complete.

Note: All the Big-O where calculated assuming a hash lookup is O(1) even though it’s really O(n). The coefficient of the n is so low, the ram overhead of storing a large enough array would hurt you before the characteristics of lookup Big-O would start taking effect. For example the difference between a call to array_key_exists at N=1 and N=1,000,000 is ~50% time increase.

Interesting Points:

isset/array_key_exists is much faster than in_array and array_search
+(union) is a bit faster than array_merge (and looks nicer). But it does work differently so keep that in mind.
shuffle is on the same Big-O tier as array_rand
array_pop/array_push is faster than array_shift/array_unshift due to re-index penalty

Lookups:

array_key_exists O(n) but really close to O(1) - this is because of linear polling in collisions, but because the chance of collisions is very small, the coefficient is also very small. I find you treat hash lookups as O(1) to give a more realistic big-O. For example the different between N=1000 and N=100000 is only about 50% slow down.

isset( $array[$index] ) O(n) but really close to O(1) - it uses the same lookup as array_key_exists. Since it’s language construct, will cache the lookup if the key is hardcoded, resulting in speed up in cases where the same key is used repeatedly.

in_array O(n) - this is because it does a linear search though the array until it finds the value.

array_search O(n) - it uses the same core function as in_array but returns value.

Queue functions:

array_push O(∑ var_i, for all i)

array_pop O(1)

array_shift O(n) - it has to reindex all the keys

array_unshift O(n + ∑ var_i, for all i) - it has to reindex all the keys

Array Intersection, Union, Subtraction:

array_intersect_key if intersection 100% do O(Max(param_i_size)*∑param_i_count, for all i), if intersection 0% intersect O(∑param_i_size, for all i)

array_intersect if intersection 100% do O(n^2*∑param_i_count, for all i), if intersection 0% intersect O(n^2)

array_intersect_assoc if intersection 100% do O(Max(param_i_size)*∑param_i_count, for all i), if intersection 0% intersect O(∑param_i_size, for all i)

array_diff O(π param_i_size, for all i) - That’s product of all the param_sizes

array_diff_key O(∑ param_i_size, for i != 1) - this is because we don’t need to iterate over the first array.

array_merge O( ∑ array_i, i != 1 ) - doesn’t need to iterate over the first array

(union) O(n), where n is size of the 2nd array (ie array_first + array_second) - less overhead than array_merge since it doesn’t have to renumber

array_replace O( ∑ array_i, for all i )

Random:

shuffle O(n)

array_rand O(n) - Requires a linear poll.

Obvious Big-O:

array_fill O(n)

array_fill_keys O(n)

range O(n)

array_splice O(offset + length)

array_slice O(offset + length) or O(n) if length = NULL

array_keys O(n)

array_values O(n)

array_reverse O(n)

array_pad O(pad_size)

array_flip O(n)

array_sum O(n)

array_product O(n)

array_reduce O(n)

array_filter O(n)

array_map O(n)

array_chunk O(n)

array_combine O(n)

I’d like to thank Eureqa for making it easy to find the Big-O of the functions. It’s an amazing free program that can find the best fitting function for arbitrary data.

EDIT:

For those who doubt that PHP array lookups are O(N), I’ve written a benchmark to test that (they are still effectively O(1) for most realistic values).

$tests = 1000000;
$max = 5000001;


for( $i = 1; $i <= $max; $i += 10000 ) {
//create lookup array
$array = array_fill( 0, $i, NULL );

//build test indexes
$test_indexes = array();
for( $j = 0; $j < $tests; $j++ ) {
$test_indexes[] = rand( 0, $i-1 );
}

//benchmark array lookups
$start = microtime( TRUE );
foreach( $test_indexes as $test_index ) {
$value = $array[ $test_index ];
unset( $value );
}
$stop = microtime( TRUE );
unset( $array, $test_indexes, $test_index );

printf( "%d,%1.15f\n", $i, $stop - $start ); //time per 1mil lookups
unset( $stop, $start );
}